Basic HTML Version
20
Il secondo Novecento
Esiste anche un’altra possibilità di modificare il quin-
to postulato e quindi la geometria euclidea. Si può
negare del tutto l’esistenza di rette parallele e soste-
nere che la
somma
degli
angoli interni di un trian-
golo
è
maggiore di 180°
.
La geometria così ottenuta si deve al matematico
Georg Friedrich Bernhard Riemann (1826-1866),
allievo di Gauss, ed è nota come
geometria ellitti-
ca
o
sferica
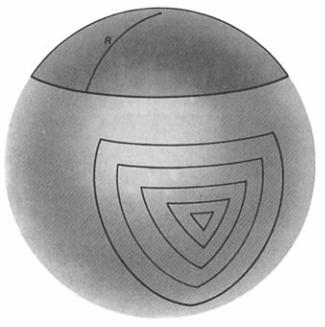
: descrive le proprietà di figure che stan-
no su una superficie che è di curvatura positiva co-
stante (vedi Figura 2).
1.1.2 Geometria e spazio fisico
Alle geometrie iperboliche ed ellittiche può essere data una
struttura assiomatica altrettanto rigorosa di quella della geometria euclidea. Il risultato de-
gli studi che conducono alla loro formulazione è dunque la possibilità, dal punto di vista
matematico, di
geometrie alternative
a quella euclidea. Questo pone tuttavia un proble-
ma fondamentale: se la geometria è la scienza dello spazio e lo spazio è inteso come quello
della nostra esperienza sensibile, non dovrebbe essere possibile più di una geometria vera.
E questa geometria dello spazio esterno era stata tradizionalmente identificata con quella
euclidea. Non solo: con la fisica di Newton lo spazio euclideo era stato identificato addirit-
tura con lo spazio fisico “assoluto”, lo scenario immobile e immateriale in cui, secondo la
concezione newtoniana, avvengono i fenomeni naturali e si svolgono i processi fisici.
Se si assume che non ci sia distinzione tra
geometria matematica
e
geometria fisica
(nel
senso di scienza dello spazio fisico), qual è dunque la geometria “vera” tra quelle matema-
ticamente possibili? Per gli scopritori delle geometrie non euclidee, la risposta doveva veni-
re dall’
esperienza
, cioè attraverso la realizzazione di opportune misurazioni. In questa di-
rezione s’inseriscono i calcoli di Gauss sulla somma degli angoli di un triangolo che ha co-
me vertici le cime di tre montagne, o quelli astronomici di Lobaˇcevskij sulla somma degli
angoli di un triangolo formato dalla Terra, dal Sole e dalla stella Sirio. Sia Gauss sia Lobaˇcevskij
ottengono risultati interpretabili nel senso di un accordo della “geometria fisica” con la ge-
ometria euclidea. Ma le distanze che si possono trovare in natura, nota Lobaˇcevskij, posso-
no essere tali che anche una distanza astronomica come quella della Terra dalla stella Sirio
può apparire trascurabile. Lobaˇcevskij ne trae la conclusione che, per quanto la geometria
euclidea rappresenti in modo appropriato lo spazio come è percepito dai nostri sensi, «non
si può garantire che non possa mostrarsi sensibilmente falsa anche prima di andare al di là
del mondo a noi visibile».
Questo
approccio empirista
al problema posto dalle geometrie non euclidee era tuttavia
in forte contrasto con la
concezione kantiana
dello
spazio
: cioè l’idea che lo spazio non
fosse «un concetto empirico, ricavato da esperienze esterne», ma «una rappresentazione ne-
cessaria
a priori
, che serve da fondamento a tutte le intuizioni esterne». Dal punto di vista
di una concezione della geometria euclidea come valida a priori (per
Kant
gli
assiomi
della
geometria euclidea
hanno lo statuto di
giudizi sintetici a priori
, valevoli universalmente
e necessariamente), non aveva certo senso cercare nell’esperienza dello spazio una risposta
alla questione di quali fossero i
veri assiomi geometrici
: gli assiomi veri erano necessaria-
mente quelli euclidei, e le geometrie alternative non rappresentavano altro che giochi logici.
FILOSOFI
A
CONFRONTO
Geometria ellittica
La posizione empirista:
Gauss e Lobaˇcevskij
Figura 2.
1_Matematica_016_099.indd 20
31/01/

