Basic HTML Version
1. Wittgenstein e la tradizione empiristica
19
E quanto è legittimo l’appello all’
evidenza
intuitiva
, una nozione di tipo psicologico piut-
tosto che logico, per garantire un fondamento solido a tutto il sistema di conoscenze ela-
borato? Nel XIX secolo, un insieme di questioni generate dagli sviluppi più avanzati della
geometria
, dell’
algebra
e dell’
analisi
mettono in crisi il criterio dell’evidenza intuitiva co-
me garanzia di verità – fino ad allora rimasto uno dei cardini del pensiero matematico –,
dando così inizio a una riflessione critica sui
fondamenti della matematica
.
Emerge progressivamente, nei vari campi della matematica, un’esigenza di chiarificazione
e determinazione dei propri metodi e concetti, che, dove si concretizza, dà origine a sua vol-
ta a nuovi e decisivi sviluppi.
1.1.1 Le geometrie non euclidee
Negli
Elementi
di Euclide il sistema assiomatico della ge-
ometria è fondato su 23 definizioni e 13 proposizioni primitive, divise in 8 assiomi, o no-
zioni comuni, e nei seguenti 5 postulati:
I
Si può condurre una linea retta da un qualsiasi punto a ogni altro punto.
II
Una retta terminata si può prolungare continuamente in linea retta.
III
Si può descrivere un cerchio con qualsiasi centro e ogni distanza.
IV
Tutti gli angoli retti sono uguali tra loro.
V
Se una retta, venendo a cadere su due rette, forma con esse angoli interni e dalla stessa parte la
cui somma è inferiore a due angoli retti, le due rette, se prolungate illimitatamente, devono ne-
cessariamente incontrarsi da quella parte.
Di questi postulati, il quinto è di ben maggior complessità concettuale degli altri e appa-
rentemente assai poco evidente. È noto anche come
postulato dell’unicità della parallela
,
in quanto di solito discusso nella formulazione che si deve a Proclo (410-485):
Data una
retta
r
e un punto
P
fuori da essa, esiste una e una sola retta s passante per
P
e parallela a
r.
Già i più antichi commentatori del testo euclideo, come Tolomeo (II secolo) e lo stesso Proclo,
manifestarono resistenze ad accettare il quinto postulato come tale, e tentarono di dedurlo da-
gli altri assiomi e postulati, ritenuti molto più intuitivi. I tentativi di dimostrazione del quinto
postulato si susseguirono senza successo nel corso dei secoli. Nel Settecento, il francese Adrien-
Marie Legendre (1752-1833) dimostrò l’equivalenza tra il quinto postulato e il seguente enun-
ciato: «La somma degli angoli interni di un triangolo piano è 180°».
Ma è solo nell’Ottocento che, dal fallimento dei tentativi di dimostrazione del quinto postu-
lato, si riesce davvero a trarre la conseguenza della
possibilità
di una
geometria non euclidea
.
I tre matematici ai quali si deve questo passo rivoluzionario sono il tedesco
Carl Friedrich
Gauss
(1777-1855), l’ungherese
János Bolyai
(1802-1860) e il russo
Nicolaj Ivanoviˇc
Lobaˇcevskij
(1793-1856). Per quanto di origini e formazione molto diverse, confrontandosi
con il problema della dimostrazione del postulato delle parallele, giungono tutti e tre a risul-
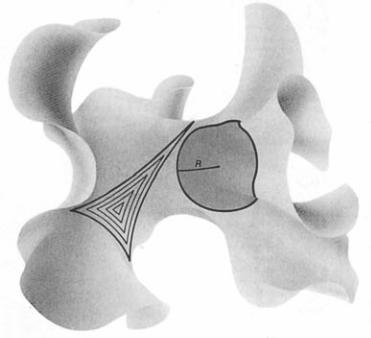
tati molto simili. Che risultato ottengono dunque Gauss, Bolyai e Lobaˇcevskij? Una geome-
tria che descrive uno spazio in cui valgono tut-
ti i postulati di Euclide, a eccezione del quinto.
Essi infatti affermano che esistono
più rette pa-
rallele
a una retta data e che la somma degli
angoli interni di un triangolo è
minore
di 180°.
La geometria così ottenuta prende il nome di
geometria iperbolica
, e descrive le proprietà
di figure che non possono stare su un piano
(cioè su una superficie di curvatura nulla, co-
me nel caso delle figure della geometria eucli-
dea) ma solo su una superficie che è di curva-
tura negativa costante (vedi Figura 1).
Esigenze di fondazione
La questione delle
rette parallele
I tentativi di
dimostrare il V
postulato
Le geometrie non
euclidee
Geometria iperbolica
Figura 1.
La somma degli angoli interni
di un triangolo è minore di 180°.
1_Matematica_016_099.indd 19
31/01/

