Basic HTML Version


Approccio algebrico
Se ricerchi algebricamente l’intersezione di due circonferenze
C
1
e
C
2
, devi
mettere a sistema le loro equazioni:
x
2
þ
y
2
þ
a
1
x
þ
b
1
y
þ
c
1
¼
0
x
2
þ
y
2
þ
a
2
x
þ
b
2
y
þ
c
2
¼
0
:
Per sottrazione trovi l’equazione lineare
a
1
a
2
ð
Þ
x
þ
b
1
b
2
ð
Þ
y
þ
c
1
c
2
ð
Þ¼
0
:
Hai ora due possibilita`:
a
1
¼
a
2
e
b
1
¼
b
2
, dunque
C
1
e
C
2
sono concentriche, infatti i centri di
C
1
e
C
2
sono
P
1
¼
a
1
2
;
b
1
2
e
P
2
¼
a
2
2
;
b
2
2
;
a
1
6
¼
a
2
oppure
b
1
6
¼
b
2
, dunque
a
1
a
2
ð
Þ
x
þ
b
1
b
2
ð
Þ
y
þ
c
1
c
2
ð
Þ¼
0 definisce
una retta.
Nel primo caso, cioe` con
C
1
e
C
2
aventi lo stesso centro, hai chiaramente che
C
1
e
C
2
coincidono oppure una delle due e` interna all’altra. Nel secondo caso
chiami invece
asse radicale
di
C
1
e
C
2
la retta di equazione
a
1
a
2
ð
Þ
x
þ
b
1
b
2
ð
Þ
y
þ
c
1
c
2
ð
Þ ¼
0, e per trovare
C
1
\
C
2
devi aggiunge-
re all’equazione di tale asse l’equazione di una qualsiasi tra
C
1
e
C
2
. Cio` spiega
perche´ l’intersezione di due circonferenze contenga al massimo due punti: coin-
cide con l’intersezione tra una circonferenza e una retta.
Le circonferenze
C
1
:
x
2
þ
y
2
þ
3
x
4
y
þ
2
¼
0 e
C
2
:
x
2
þ
y
2
þ
x
5
y
þ
4
¼
0
hanno asse radicale 2
x
þ
y
2
¼
0, ovvero
y
¼
2
ð
1
x
Þ
. Sostituendo nell’equazione di
C
1
trovi 5
x
2
þ
3
x
2
¼
0, che ha le soluzioni
x
¼
1 e
x
¼
2
5
, dunque
C
1
e
C
2
hanno i punti di intersezione
ð
1
;
4
Þ
e
2
5
;
6
5
.
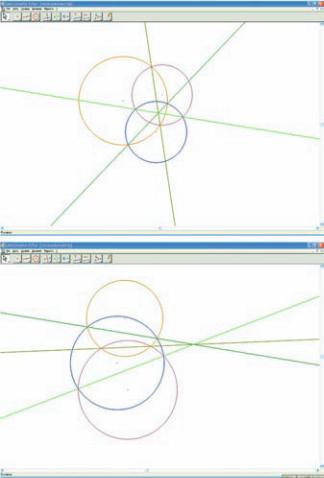
Con Cabri puoi dare una ‘‘dimostrazione sperimentale’’ del
seguente teorema:
Prendi tre circonferenze
C
1
,
C
2
,
C
3
a coppie
secanti. Per ogni coppia traccia l’asse radicale, cioe` la retta che contiene i
loro punti di intersezione. Allora i tre assi radicali si incontrano in un
punto
. Dopo avere lanciato il programma clicca sul tasto
Circonferenza
e tracciane tre, che siano a coppie secanti. Per
distinguerle puoi dare loro colori diversi cercando sotto il menu`
del tasto piu` a destra il comando
Colore...
Ora seleziona il
tasto
Retta
, clicca uno dopo l’altro sui due punti di intersezione
di due delle circonferenze, in modo che compaia il loro asse
radicale. Ripetendo l’operazione per le altre due coppie di
circonferenze ottieni gli altri due assi radicali, e verifichi che in
effetti i tre assi hanno un punto in comune. Per controllare che
non si tratta di un caso puoi ora ‘‘animare’’ la tua figura,
cambiando centri e raggi delle tue circonferenze. Per i centri usi
lo strumento
Puntatore
del menu` piu` a sinistra, e per i raggi
usi
Dilata
dello stesso menu` . Ricorda che per accedere a un
menu` devi cliccare sulla piccola freccina nera dentro un tasto.
Mentre cambi una circonferenza vedrai muoversi due dei tre
assi, ma osserverai che il loro punto di intersezione scorre sul
terzo asse. Due delle figure che potresti ottenere sono a lato.
e
UNITA` 7
La circonferenza
305
INTERSEZIONE
DI TRE ASSI
RADICALI
Asse radicale di due
circonferenze
–1
O
x
–2 –3
1
1
2
3
4
y
–1
5

